
日本の水処理技術は非常に高いと呼ばれているけど、具体的にどのような技術があるんだろう?

小学校の頃に水処理施設へ工場見学に行った事がある方もいると思いますが、水処理技術は化学工学と密接に関わっています。
そこで、こちらの記事では…
- 水処理についてどんな技術があるのか知りたい方に向けて
- 水を綺麗にするために使われている5つの分離技術
水処理には微生物処理、UVによる殺菌、オゾン酸化による分解もありますが、今回は分離技術に絞って紹介します。
水処理技術は化学工学の集合体
利用されている分離技術
- イオン交換
- 吸着
- 膜分離
- ろ過
- 沈降・浮上・遠心分離
化学工業でプロセスを合理化するために使われる化学工学ですが、水処理技術にも至る所で化学工学の知見が使われています。
特に、分離技術については上記の5つが主に利用され、その分離技術により磨かれた水が、あらゆる産業で利用されています。
下記には、5つの分離技術の原理と何を分離しているのかを紹介します。
イオン交換
- イオン交換樹脂を利用して水中のイオン状物質を除去
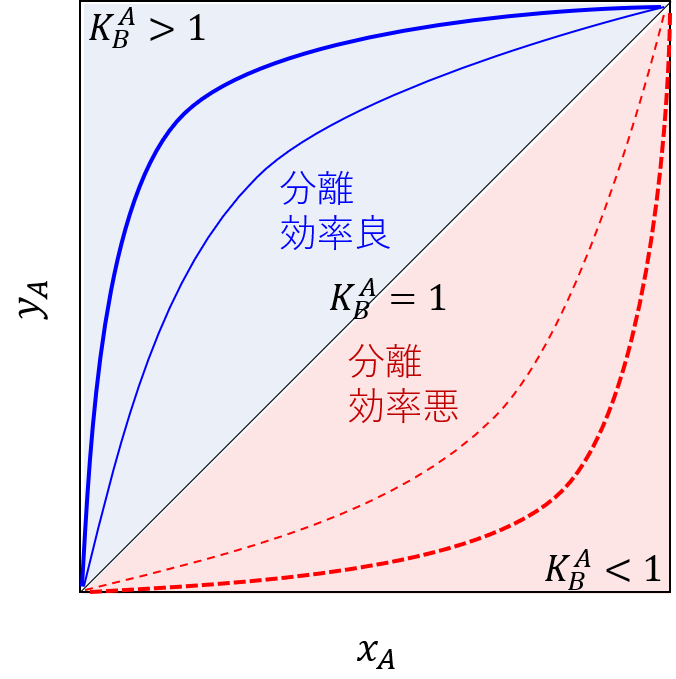
- 樹脂と水中のイオンには平衡関係が働くため、平衡定数の数値から分離可否を判断する
- 陽イオン交換樹脂にはスルホン基、陰イオン交換樹脂にはアミノ基が導入されている
- ボイラー用水&熱交換器の冷却水の軟化処理には陽イオン交換樹脂を利用
- 純水製造には陽・陰イオン交換樹脂を利用
基礎式は下記のアイコンをクリックして展開することで、表示できます。

イオン交換樹脂の構造の例
溶液中のイオンとイオン交換樹脂の末端(H+ or OH–)が、水中のナトリウムなどの陽イオン or 塩素などの陰イオンと交換することで、溶液中のイオンを分離できます。
吸着
基礎式は下記のアイコンをクリックして展開することで、表示できます。
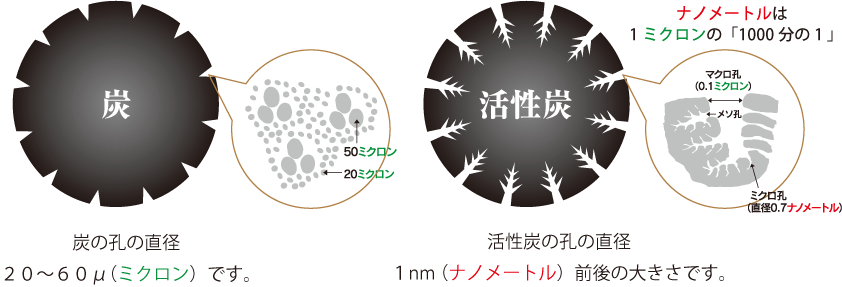
引用:株式会社MET 炭と活性炭の違い
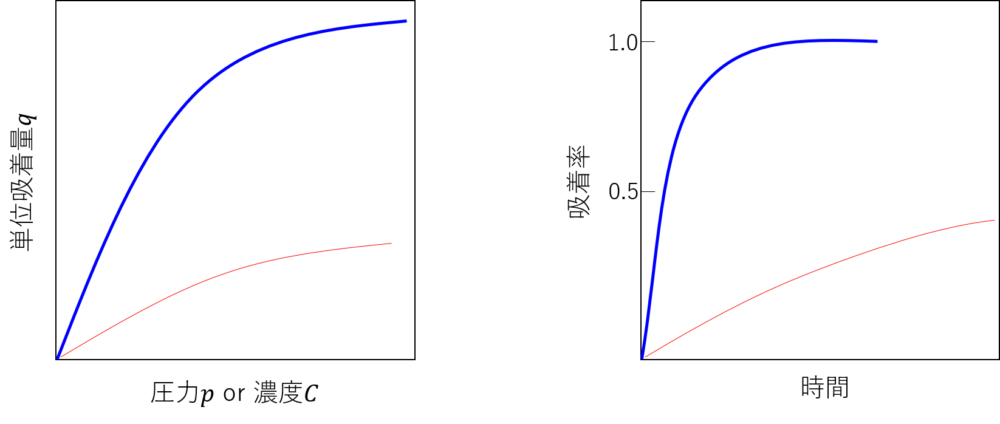
活性炭には細孔部に反応活性があり、それを利用して物質を吸着できます。
また、この細孔の大きさによって、吸着特性が異なります。
膜分離
- 膜を介して物質移動が生じる事を利用して、溶液中のイオン、タンパク質、ウィルスなどを除去
- 透過速度差によって分離するため、溶質サイズ・分子量の差から分離可否を判断する
- 分離したいものの大きさによって、選択する膜が異なる
膜分離の詳細は以下の記事をご参照ください。
ろ過
- メンブレン・不織布などのろ材を利用して、微粒子、微生物、コロイド状物質などの固体を除去
- 粒子サイズによって分離するため、ろ材の孔径から分離可否を判断する
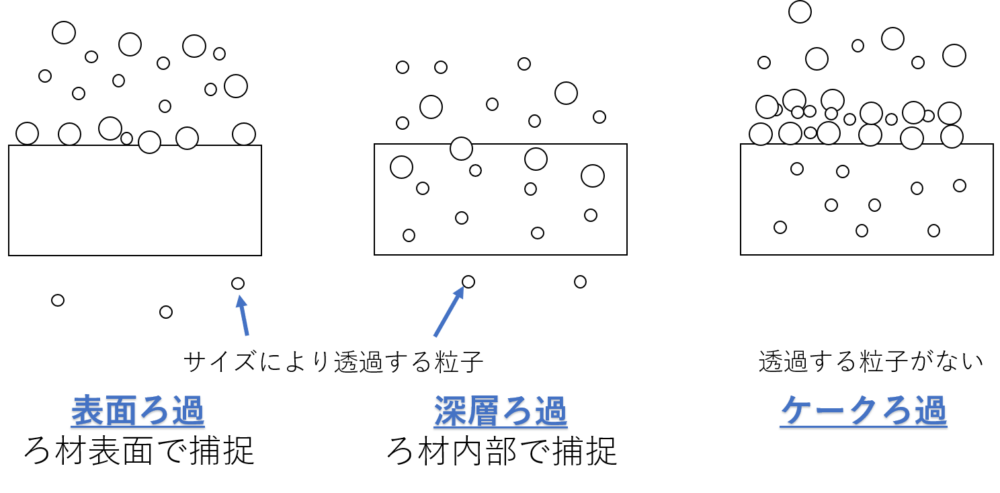
- ろ過形式には表面ろ過、深層ろ過、ケークろ過の捕捉モデルがある
- 不織布の材質には、ポリプロピレンやポリエステルを使用
- 排水や下水の固形物除去に利用されている
基礎式は下記のアイコンをクリックして展開することで、表示できます。

沈降・浮上・遠心分離
共通の原理
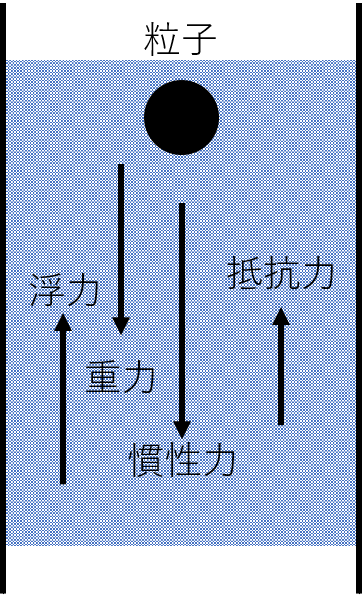
- 流体中の固体物質そのものを沈降もしくは浮上させる事によって、微粒子を除去
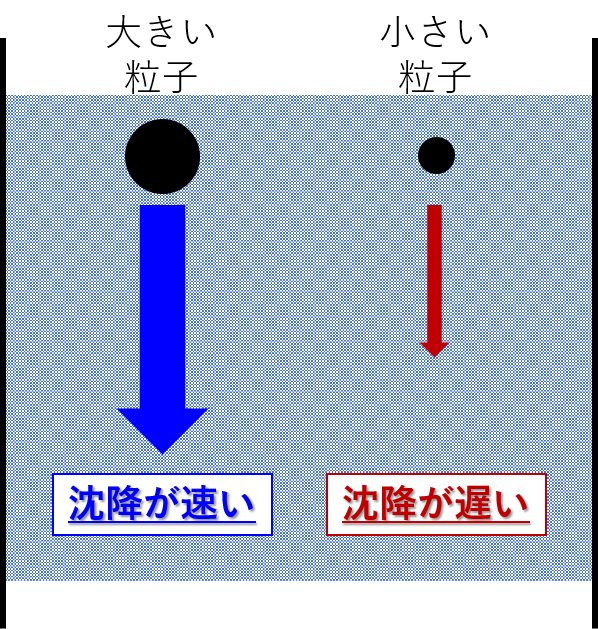
- 流体中の移動速度の差によって分離するため、粒径、流体・粒子の密度、流体の粘性から分離可否を判断する
- 微粒子の分離にはろ過を含め様々な手段がある
☞ 推進力の大きさが分離効率を高めるため、最も推進力が大きい手段を選択する
基礎式は下記のアイコンをクリックして展開することで、表示できます。
沈降

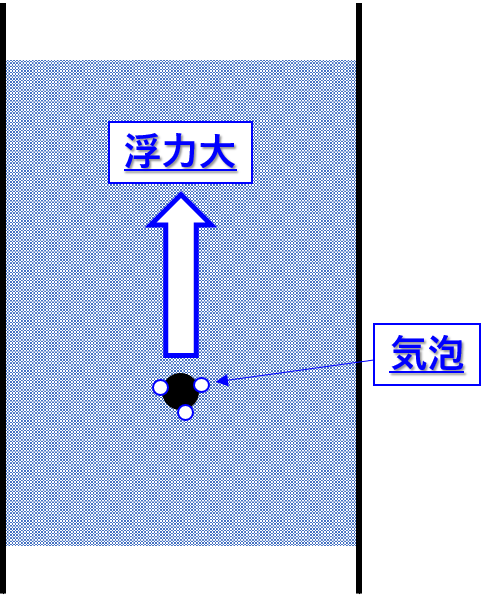
浮上
- フロックに泡を付着させ、泡の浮力でフロックを浮かせる
- 泡の浮力が沈降に比べて非常に大きければ、沈降分離槽より浮上分離槽を小さくできる
- 泡は数~数十µmのマイクロバブルを使用
- 泡の発生方法
① 0.3~0.7 MPaに加圧した水に圧縮空気を混合し、空気を溶解
☞ 気体の溶解度はヘンリーの法則を利用
② 空気を溶解した加圧水を廃水フローへ投入すると、圧力が大気開放
③ 水へ溶解しきれなくなった空気がマイクロバブルとなって析出

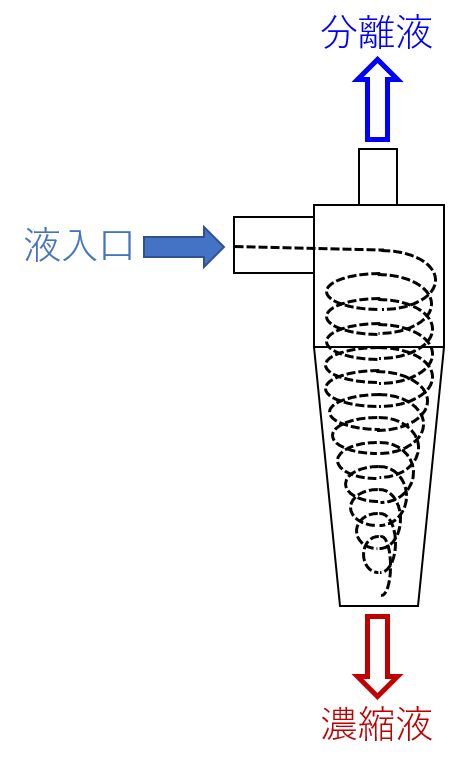
遠心分離(サイクロン)
- 遠心力を利用して液体中の固形物を除去する
- 共通原理の物性に加えて、周速が大きく影響する
- 小さい粒子を分離する場合、入口流速を上げる or 内径を小さくして周速を上げる

まとめ
今回は、「水処理に利用される5つの分離技術」をテーマに紹介しましたが、いかがでしたでしょうか?
- 水処理の分離技術にはイオン交換、吸着、膜分離、ろ過、沈降・浮上・遠心分離の5つがある
- 5つの分離技術それぞれで、分離する対象物が異なる
☞ 求められている水質によって、採用する分離手段が異なる - 対象物に応じて、各段階で最も推進力が大きい分離手段をプロセスに入れる
SDGsに関連する新規分離技術について知りたい方は、下記の記事を参照ください。


最後までご覧いただき、ありがとうございました!





コメント